Per descrivere alcuni fenomeni in modo esaustivo non è sufficiente utilizzare grandezze fisiche puramente numeriche, ma è necessario introdurre un diverso oggetto matematico. Un esempio di questa necessità è rappresentato, ad esempio, dalla descrizione di un moto che si svolge sul piano e non su una retta come abbiamo visto qui. Infatti quando dobbiamo descrivere il moto in due dimensioni (o in tre se parliamo di moto nello spazio) possiamo avere il bisogno di descrivere una traiettoria del genere:
In questo caso abbiamo un moto separato in tre parti:
1. lungo il segmento a (nel verso indicato dalla freccia) per una distanza di 4 m
2. lungo il segmento b per una distanza di 3 m
3. lungo il segmento c la cui lunghezza, dato che a e b formano un angolo di 90°, risulta calcolabile con il teorema di Pitagora 
da cui 
Possiamo quindi descrivere la distanza totale percorsa come la somma delle distanze percorse nei tre segmenti a, b e c ottenendo una distanza totale d pari a 12m.
Ma riusciamo a sapere di quanto ci siamo spostati mediante questo calcolo? Se consideriamo lo spostamento, infatti, osserviamo che la posizione iniziale corrisponde con la posizione finale e quindi lo spostamento totale è zero. Dunque il calcolo eseguito non è una descrizione esauriente del moto indicato in figura, poiché ci restituisce solo la distanza effettivamente percorsa ma non tiene adeguatamente in considerazione il fatto che lo spostamento totale è nullo. Quello che il calcolo non riesce a considerare è l’orientamento dei singoli segmenti, che in questo caso formano una traiettoria chiusa e dunque uno spostamento nullo.
L’orientamento dei singoli segmenti è invece una caratteristica fondamentale per descrivere il moto in due dimensioni, prendendo infatti gli stessi segmenti e posizionandoli diversamente otteniamo traiettorie diverse che, a fronte di una distanza totale sempre uguale a 12m, corrispondono a spostamenti diversi.
Come facciamo quindi ad avere una descrizione matematica del moto sul piano e calcolare lo spostamento? Calcolo che nel primo caso deve dare come risultato a + b + c = 0 (e quindi 4 + 3 + 5 = 0).
L’oggetto matematico che rappresenta lo spostamento e tiene dunque conto sia della lunghezza che dell’orientamento del segmento che lo rappresenta è il vettore. Il vettore è dunque rappresentato non solo da un valore numerico (la lunghezza del segmento), ma anche da una direzione (la retta lungo la quale è posizionato il segmento) e da un verso (l’orientamento del segmento). Il valore numerico è anche detto intensità o modulo del vettore. Il vettore viene indicato da una lettera con sopra una piccola freccia (ad esempio 
), la stessa lettera senza la freccia indica il modulo del vettore. Con questo nuovo oggetto possiamo tornare a studiare la nostra operazione precedente in cui lo spostamento totale è rappresentato correttamente dalla somma vettoriale 
.
Ma come si effettua la somma tra vettori? Ci sono diverse possibilità. Ci sono due diversi metodi geometrici e un metodo analitico (numerico).
Il metodo punta-coda
Per sommare due vettori con il metodo punta-coda dobbiamo trasportare la coda del secondo vettore sulla punta del primo (senza cambiare né la lunghezza né l’inclinazione dei due vettori). La somma è data da un vettore la cui coda coincide con la coda del primo vettore e la cui punta coincide con la punta del secondo vettore, come si vede bene dal vettore spostamento.
Il metodo del parallelogramma
In questo secondo metodo geometrico dobbiamo invece trasportare il secondo vettore in modo che la sua coda corrisponda con la coda del primo vettore. A questo punto dobbiamo tracciare la retta parallela al secondo vettore passante per la punta del primo vettore e la retta parallela al primo vettore passante per la punta del secondo vettore. La somma vettoriale è data da un vettore che inizia nel punto in cui sono posizionate le due code e termina nel punto di incontro delle rette parallele.
Il metodo analitico
Per applicare questo metodo dobbiamo prima di tutto introdurre una nuova rappresentazione dei vettori. Disegniamo ogni vettore in un piano cartesiano, con la coda nell’origine degli assi (il punto 0,0). Il vettore sarà rappresentato allora dalla coppia di numeri corrispondente alle coordinate x e y della punta del vettore. Queste coordinate si dicono anche componenti del vettore. Prendendo come esempio i vettori dello spostamento originale abbiamo ad esempio
La somma vettoriale 
è un vettore le cui componenti sono la somma delle componenti di 
e di 
.
Si vede che il vettore somma 
è lo stesso che avremmo ottenuto utilizzando uno dei due metodi geometrici illustrati in precedenza. ATTENZIONE: Bisogna sempre posizionare la coda del vettore nell’origine degli assi del piano cartesiano.
Componenti negative
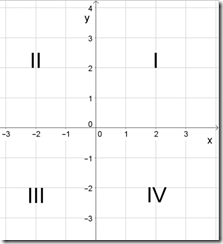
In un piano cartesiano ci sono alcune zone (chiamate quadranti) in cui una o più coordinate sono negative.
Nel I quadrante x e y sono entrambi positive, nel II quadrante la coordinata x è negativa mentre la y è positiva, nel III quadrante sia x che y sono negative, nel IV quadrante la x è positiva e la y è negativa. Alcuni vettori sono orientati in modo che la loro punta cada in uno di questi quadranti. In questo caso alcune o tutte le loro componenti corrispondono a coordinate negative. In questo caso l’eventuale segno negativo va riportato all’interno delle componenti e ne va tenuto conto al momento di fare la somma vettoriale, sommando o sottraendo a seconda del segno. Allo stesso modo va disegnato correttamente l’eventuale risultato con componenti negative.
In questo caso la somma vettoriale è
Esercizio
Utilizzando i tre metodi illustrati, verificare che lo spostamento totale dell’esempio iniziale dia come risultato un vettore nullo (in cui coda e punta coincidono).
Casi particolari
Calcolare la somma vettoriale, utilizzando i tre metodi illustrati, di due vettori con stessa intensità, stessa direzione ma verso opposto. Cosa osserviamo?
Materiale
Potete scaricare la versione word di questa lezione da qui (http://1drv.ms/1ncto6k).
I disegni dei vettori sono stati fatti con Geogebra.
Background noise 